Retornos pasados no garantizan retornos futuros
¿Te suena? La advertencia está en esa frase que dicen muy rápido al final de los comerciales de los bancos en la radio.
Y tiene sentido, nada garantiza que algo que ya pasó se va a repetir en el futuro. En inversiones si un activo sube mucho de precio, puede ser que ese instrumento ahora esté “caro” y su retorno potencial futuro ahora sea más bajo (a menos que su valor haya subido realmente).
Por lo mismo en Fintual no intentamos predecir el futuro. Como lo hemos comentado en otras ocasiones, nuestra filosofía de inversiones es más bien pasiva, ya que es lo que históricamente ha funcionado mejor en mercados globales.
Sin embargo, muchas veces las personas necesitan saber una proyección que nos muestre más o menos cómo se comportará su inversión en el futuro. Por ejemplo, es útil entender cómo evolucionaría esa inversión en caso de escenarios negativos. O también es interesante visualizar el trade-off entre el riesgo y el retorno dentro de las distintas combinaciones de fondos que ofrecemos en Fintual: mientras más arriesgado sea el portafolio que simule, mayor será el retorno esperado en el futuro.
Es por esto que tenemos un simulador que seguramente has visto al momento de crear tus objetivos en Fintual.
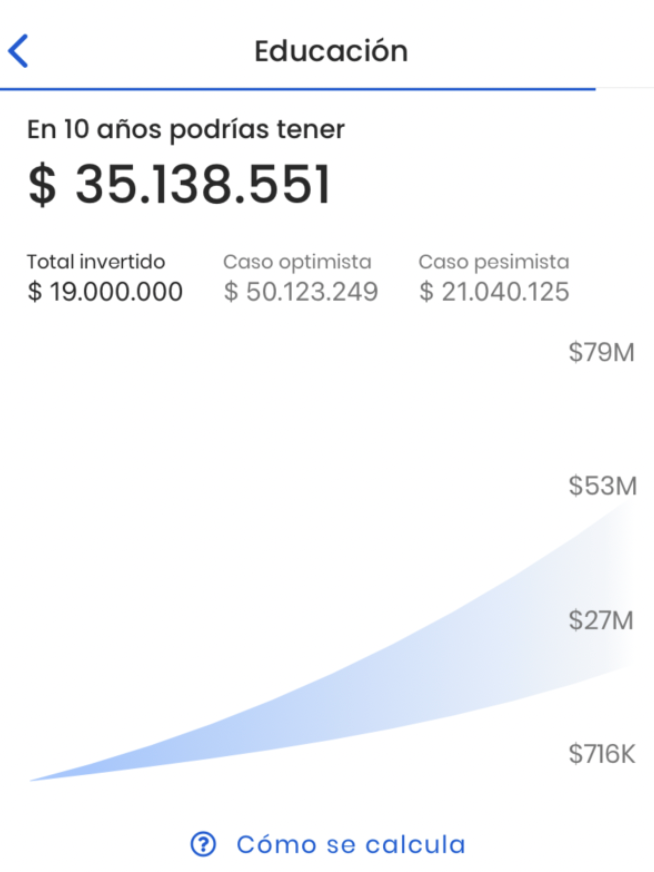
El simulador intenta dar una proyección de cómo evolucionaría tu ahorro bajo distintos supuestos y escenarios, lo que se muestra en el área azul. Si se dan los escenarios más negativos, rondarías los montos inferiores de ese triángulo. Y si se dan escenarios buenos, rondarías la parte superior del área.
Como te comentaba, esta simulación tiene supuestos. Toda proyección de retornos tiene que asumir ciertos parámetros que determinen el comportamiento de los activos en el largo plazo, tanto para las acciones como para la renta fija. Esos supuestos se usan como insumos para estimar los resultados del simulador.
En su expresión más básica, la teoría financiera describe que el precio de un instrumento financiero depende de 2 cosas: el nivel de la tasa libre de riesgo y un premio por riesgo adicional que los inversionistas exigen por tener ese instrumento. A mayor riesgo, un inversionista debería exigir un mayor retorno.
1. Tasa libre de riesgo
La tasa libre de riesgo corresponde al interés que paga un instrumento financiero que no tiene ningún riesgo asociado.
En la práctica, se suele utilizar como medida libre de riesgo para los depósitos que uno puede realizar en el Banco Central, ya que no conllevan ningún riesgo crediticio (el Central emite dinero para pagar estos depósitos, por lo que es imposible que no pague). Esas tasas son similares a las tasas de política monetaria de cada banco central. Aunque estas tasas son de muy corto plazo, igual podemos extraer la expectativa de estas tasas libres de riesgo para plazos mayores en los mercados de renta fija.
Volviendo a nuestro simulador, podemos darle como input de activo libre de riesgo al valor de las tasas de interés del Banco Central, ya que es una variable observable en el mercado del día a día.
2. Premios por riesgo
Premios por riesgo históricos
A cualquier instrumento con riesgo, le vamos a exigir un retorno superior al activo libre de riesgo. A ese exceso de retorno le llamamos premio por riesgo. Si quisiéramos simular el retorno total de los instrumentos, bastaría con sumar a la tasa libre de riesgo el premio por riesgo asociado a ese activo.
Por ejemplo, si un ETF tiene un premio por riesgo de 6 % anual, y la tasa libre de riesgo es 2 % anual, entonces su retorno esperado para el futuro será de 2 % + 6 % = 8 % en un año.
El problema es que el premio por riesgo de la mayoría de los activos, como las acciones, no es una variable observable. Es decir, no puedes obtener su valor directamente de los mercados financieros sin asumir algún modelo o supuesto.
La metodología más común y simple para estimar el premio por riesgo de un instrumento consiste en calcular el premio por riesgo histórico promedio. El premio por riesgo histórico sí es observable, y para obtenerlo basta con calcular la diferencia entre el retorno histórico del instrumento y el retorno histórico del activo libre de riesgo. Esta diferencia anualizada corresponde al premio por riesgo histórico.
Por ejemplo, el siguiente gráfico muestra el premio por riesgo histórico anual de algunos índices accionarios.
Como ya habíamos mencionado, toda metodología tiene supuestos. En el caso del premio por riesgo histórico, el supuesto es que el retorno de los instrumentos por sobre la tasa libre de riesgo (su premio por riesgo) en el futuro será igual a su valor promedio del pasado.
El problema de esta metodología es que va en contra de lo primero que dijimos al principio de este artículo. Por ejemplo, si una acción hubiese subido mucho de precio —sin un cambio en sus fundamentales financieros— entonces ahora debiese estar más cara y por ende su retorno esperado debiese ser más bajo. Sin embargo, si usamos premios por riesgo históricos, las acciones que más han rentado tendrán un retorno esperado futuro mayor, lo que va contra la intuición descrita anteriormente.
Premios por riesgo implícitos
Una metodología que sí captura la intuición anterior es la de premios por riesgo implícitos.
El espíritu detrás de este modelo es que el precio actual de un activo financiero refleja la suma de todos los intereses que entregará en el futuro (dividendos si es una acción o cupones en el caso de los bonos), descontados a una tasa de descuento. Esta tasa de descuento representa el retorno futuro del activo, y es inversamente proporcional a su precio (si la tasa sube, el precio será menor).
En el caso de las acciones, el premio implícito no es observable y debemos estimarlo a partir de sus dividendos. Si tenemos el precio de mercado y todos los dividendos futuros, podemos despejar el retorno esperado implícito que el mercado está esperando que ese activo tenga. A este modelo se le conoce como modelo de dividendos descontados.
De esta manera, si el precio baja y sus dividendos futuros se mantienen constantes, entonces su retorno esperado sube, que es precisamente el efecto que buscamos. Con el modelo de premios por riesgo históricos, el retorno y premio esperado habría sido menor.
Otro punto importante es que el retorno esperado no depende de ninguna variable del pasado. Esto tiene sentido con lo que dice la teoría económica: los precios actuales solo incorporan expectativas futuras del mercado, el pasado no debiese determinar los retornos.
Pero en este modelo también tenemos supuestos. Necesitamos todos los dividendos futuros. Es decir, hay que suponer cómo evolucionarán los dividendos por acción que entregará la compañía. Aunque no tenemos cómo saber esa información con certeza, podemos apoyarnos en las proyecciones que hacen distintas casas de analistas a lo largo del mundo, y obtener una trayectoria de dividendos futuros que represente el consenso de mercado.
En cuanto a la renta fija el retorno implícito sí es una variable observable, lo que hace más fácil el cálculo. Esto es así, ya que los cupones futuros vienen predeterminados al momento de emitir un bono. Luego, la tasa de interés que se despeja de la ecuación solo trae como supuesto el hecho de que no haya algún default de los intereses o el principal de la deuda (efectivamente, se pague todo lo que se comprometió al momento de comprar el bono). Después se pueden hacer ajustes incorporando estimaciones de tasas de default y tasas de recuperación, en caso de bonos que tengan incorporados riesgos de crédito o no pago.
Bajada a Fintual
El simulador actual de Fintual se basa en la metodología de premios por riesgo implícitos. Para obtener el vector de dividendos futuros, nos nutrimos del consenso de analistas que reportan a Bloomberg —la plataforma financiera más grande del mundo— y su modelo propietario de proyección de dividendos de largo plazo para acciones de los principales índices bursátiles de cada país (como el S&P 500). La ventaja de esto es su amplitud y diversidad: se nutre de una diversa base de analistas a lo largo del mundo, que entregan proyecciones compañía por compañía, para luego agregarlas al país.
Con base en la estimación de premio por riesgo implícito que tenemos para cada país, calculamos el premio por riesgo de cada ETF basándonos en un modelo lineal, o Capital Asset Pricing Model (CAPM). Aquí utilizamos como retorno esperado para el mercado, al premio por riesgo implícito calculado para el país donde invierte el ETF en cuestión.
En esta fórmula, la sensibilidad al mercado se obtiene a base de una regresión lineal histórica entre el premio por riesgo histórico del ETF y el índice representativo del país. De esta manera, basándonos en los premios por riesgo de cada país, podemos estimar el retorno esperado de cualquier ETF que tenemos en cartera.
Una vez que obtenemos las estimaciones de retornos según la metodología de premios implícitos, podemos corregir el nivel de la distribución de retornos históricos.
Lo importante de esta metodología es que nos permite estimar valores razonables de riesgos esperados, calibrados según un nivel de mercado o consenso, ya sea con el nivel de tasas de mercado o con el consenso de analistas que reportan a Bloomberg. Pero, al mismo tiempo, no implica ninguna hipótesis sobre correlaciones de activos, dependencia lineal, o supuestos de distribuciones de retornos de activos a la hora de estimar escenarios extremos, y por lo tanto, los escenarios optimistas y pesimistas conservan las propiedades de eventos reales de mercado experimentados en la historia.
Literatura
Tanto la estimación de premios por riesgo como el CAPM, son modelos que ya llevan años de estudio en la academia.
Por un lado, el modelo de dividendos descontados en su versión extendida fue propuesto por el académico Myron J. Gordon de la Universidad de Toronto en 1962. Por otro lado, el cálculo de los premios por riesgo implícitos han sido en gran parte estudiados por el profesor Aswath Damodaran de la Universidad de Nueva York. En su trabajo, detalla las distintas formas de calcularlo, sus ventajas y desventajas.
En cuanto al CAPM, es un modelo clásico de teoría financiera. Sus orígenes se remontan a la década de 1960, donde diversos académicos —entre ellos el premio nobel de economía William Sharpe— sentaron las bases para la teoría de asset pricing a través de esta sencilla pero importante metodología.
Si te gustó este artículo y tienes un comentario o algo para complementarlo, escríbenos a cartas@fintual.com. Publicamos las más destacadas.